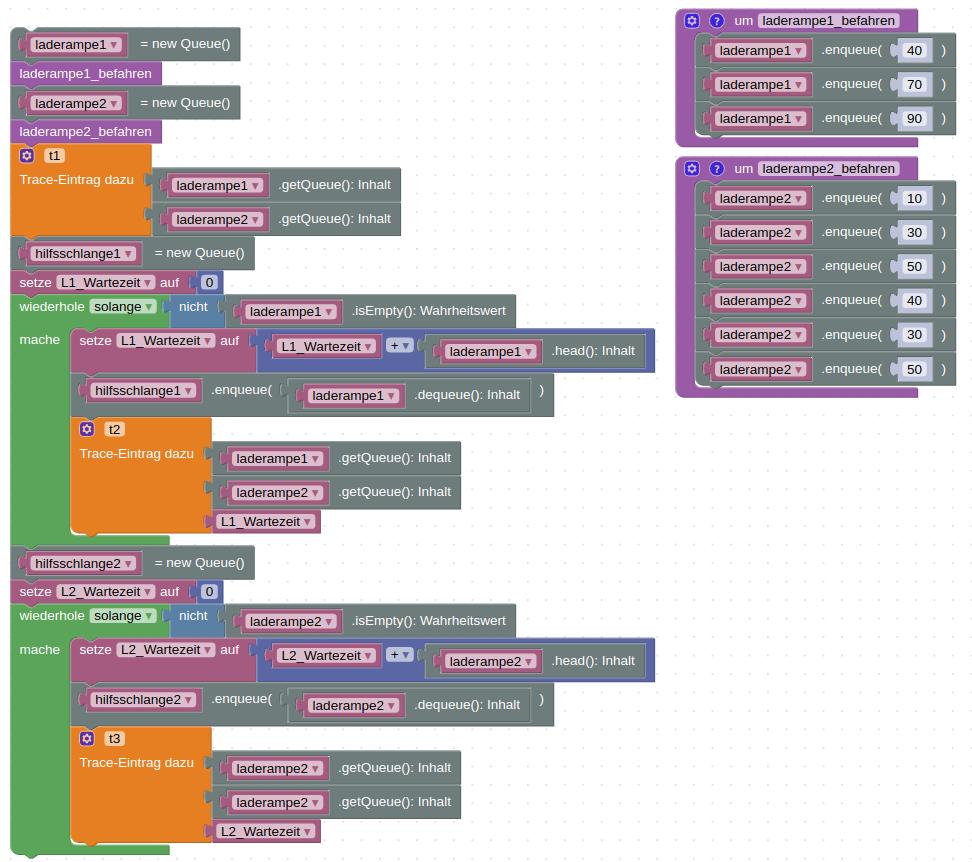
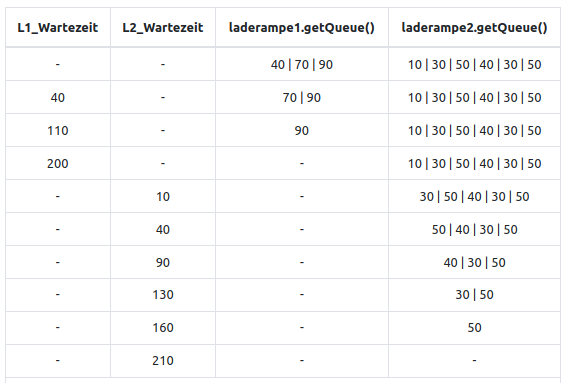
Damit ein Binärbaum entstehen und auch ausgegeben werden kann, müssen einige Algorithmen ergänzt werden. Im folgenden wird beispielhaft gezeigt, wie eine Objektschablone (Klasse) gewichteterSortierterBinaerBaum() für einen sortierten gewichteten Binärbaum programmiert werden kann. Dabei bedeutet:
-
sortiert: wenn ein neuer Wert in den Binäbaum eingefügt wird, kommt er nach links, wenn er kleiner als der Wert im Knoten ist. Ist er größer als der Wert im Knoten, kommt er nach rechts. Auf diese Weise wird der richtige Platz im Binärbaum für den neuen Wert gesucht.
-
da die Eingabe von Werten in einen sortierten Binärbaum oft zufällig ist, kann ein ungewichteter Binärbaum unsymmetrisch aussehen:
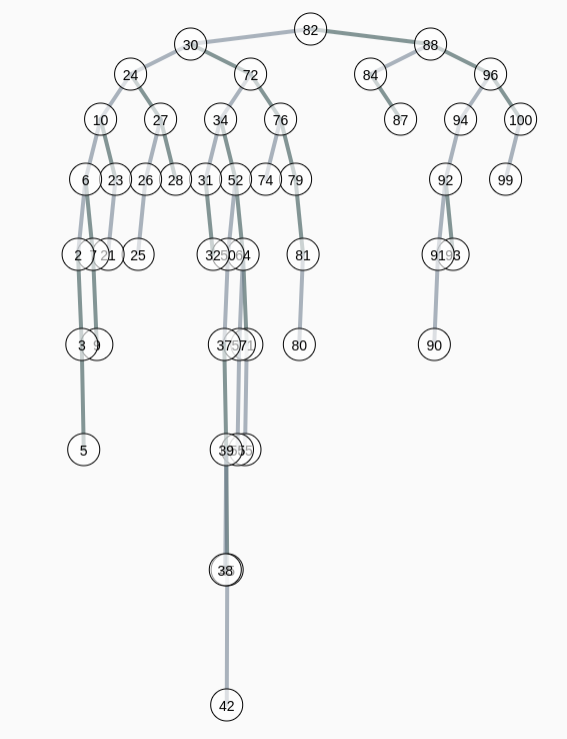
- Bei einem gewichteten Binärbaum werden Operationen ergänzt, mit welchen die Werte im Binärbaum so verteilt werden, dass der Baum möglichst symmetrisch relativ zur Wurzel ist:
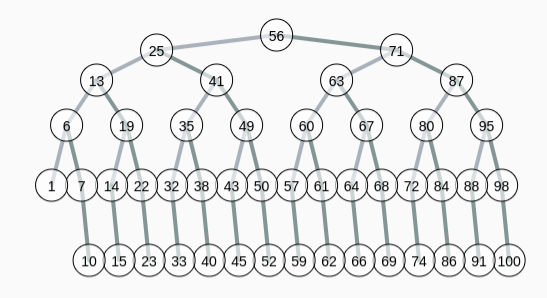
Eine Klasse gewichteterSortierterBinaerBaum() kann mit Hilfe des ADTs Binärbaum wie folgt festgelegt werden:
class BinTree {
constructor(inhalt) {
this.inhalt = inhalt;
this.links = null;
this.rechts = null;
}
isLeaf() { return (this.links === null && this.rechts === null); };
getLeft() { return this.links; };
getRight() { return this.rechts; };
setLeft(knot) { this.links = knot; };
setRight(knot) { this.rechts = knot; };
getItem() { return this.inhalt };
setItem(val) { this.inhalt = val };
}
class gewichteterSortierterBinaerBaum {
constructor() {
this.wurzel = null;
}
knotenEinfuegen(knoten, neuerKnoten) {
if (neuerKnoten.getItem() < knoten.getItem()) {
if (knoten.getLeft() === null) { knoten.setLeft(neuerKnoten); }
else { this.knotenEinfuegen(knoten.getLeft(), neuerKnoten); }
}
if (neuerKnoten.getItem() > knoten.getItem()) {
if (knoten.getRight() === null) { knoten.setRight(neuerKnoten); }
else { this.knotenEinfuegen(knoten.getRight(), neuerKnoten); }
}
};
inhaltEinfuegen(inhalt) {
var neuerKnoten = new BinTree(inhalt);
if (this.wurzel === null) { this.wurzel = neuerKnoten; }
else { this.knotenEinfuegen(this.wurzel, neuerKnoten); }
};
findeMinKnoten(knoten) {
if (knoten.getLeft() === null) return knoten;
else return this.findeMinKnoten(knoten.getLeft());
};
knotenEntfernen(knoten, zahl) {
if (knoten === null) { return null;
} else if (zahl < knoten.getItem() && knoten.getLeft() != null) {
knoten.setLeft(this.knotenEntfernen(knoten.getLeft(), zahl));
return knoten;
} else if (zahl > knoten.getItem() && knoten.getRight() != null) {
knoten.setRight(this.knotenEntfernen(knoten.getRight(), zahl));
return knoten;
} else if (zahl === knoten.getItem()) {
if (knoten.getLeft() === null && knoten.getRight() === null) {
knoten = null; return knoten;
}
if (knoten.getLeft() === null && knoten.getRight() != null) {
knoten = knoten.getRight(); return knoten;
}
if (knoten.getRight() === null && knoten.getLeft() != null) {
knoten = knoten.getLeft(); return knoten;
}
if (knoten.getRight() != null && knoten.getLeft() != null) {
var bleibtDa = this.findeMinKnoten(knoten.getRight());
knoten.setItem(bleibtDa.getItem());
knoten.setRight(this.knotenEntfernen(knoten.getRight(), bleibtDa.getItem()));
return knoten;
}
} else return knoten;
}
inhaltEntfernen(inhalt) {
this.wurzel = this.knotenEntfernen(this.wurzel, inhalt);
};
maxTiefefunction() {
var tiefeBerechnen = function(knoten) {
if (knoten === null) return 0;
return Math.max(1 + tiefeBerechnen(knoten.getLeft()), 1 + tiefeBerechnen(knoten.getRight()));
}
return tiefeBerechnen(this.wurzel);
};
knotenArrSpeichern(knoten, knotenArr) {
if (knoten == null) return;
this.knotenArrSpeichern(knoten.getLeft(), knotenArr);
knotenArr.push(knoten);
this.knotenArrSpeichern(knoten.getRight(), knotenArr);
};
bGewichtHelfer(knotenArr, start, ende) {
if (start > ende) return null;
var mitte = parseInt((start + ende)/2, 10);
var knoten = knotenArr[mitte];
knoten.setLeft(this.bGewichtHelfer(knotenArr, start, mitte - 1));
knoten.setRight(this.bGewichtHelfer(knotenArr, mitte + 1, ende));
return knoten;
};
baumGewichten(wurzel) {
var knotenArr = [];
this.knotenArrSpeichern(wurzel, knotenArr);
var n = knotenArr.length;
return this.bGewichtHelfer(knotenArr, 0, n-1);
};
};
In der Klasse gewichteterSortierterBinaerBaum sind einige rekursive Operationen enthalten. Eine rekursive Operation ruft sich selbst bei der Ausführung des Programms auf. Mit Hilfe des rekursiven Programmieransatzes kann ein Binärbaum gebaut werden, bei welchem zum Zeitpunkt der Festlegung des Binärbaums unbekannt ist, welche Tiefe er haben wird. Ausgegeben wird der Binärbaum mit der Operation bDrucker(asb, xT, yT, level, dX), die ebenfalls eine rekursive (sich selbst aufrufende) Operation ist, damit ein unsymmetrischer Binärbaum unbekannter Tiefe ausgegeben werden kann:
function bDrucker(asb, xT, yT, level, dX) {
let yDeltaD = 15;
let yDL = 0;
if (asb.rechts != null) {
yDL = yDeltaD*level;
push();
stroke(47, 79, 79, 150);
strokeWeight(4);
line(xT, yT, xT+dX, yT+yDL);
pop();
bDrucker(asb.rechts, xT+dX, yT+yDL, level+1, dX/2);
}
if (asb.links != null) {
yDL = yDeltaD*level;
push();
stroke(112, 128, 144, 150);
strokeWeight(4);
line(xT, yT, xT-dX, yT+yDL);
pop();
bDrucker(asb.links, xT-dX, yT+yDL, level+1, dX/2);
}
fill(255, 255, 255, 150);
ellipse(xT, yT, 32, 32);
fill(0);
textSize(14);
textAlign(CENTER);
text(asb.inhalt, xT, yT+6);
}
Angelegt wird ein sortierter Binärbaum mit folgender Anweisung:
let binaerBaumVar = new gewichteterSortierterBinaerBaum();
In den Binärbaum werden mit folgender Anweisung 60 Elemente sortiert eingefügt:
for (var count = 0; count < 60; count++) {
binaerBaumVar.inhaltEinfuegen((mathRandomInt(1, 100)));
}
Mit folgender Anweisung wird der sortierte Binärbaum gewichtet, was bedeutet, dass die Elemente symmetrisch zur Wurzel angeordnet werden:
binaerBaumVar.wurzel = binaerBaumVar.baumGewichten(binaerBaumVar.wurzel);
Ein funktionsfähiges Beispiel für einen sortierten gewichteten Binärbaum ist folgendes Programm. Entfernt man die Zeile 115
binaerBaumVar.wurzel = binaerBaumVar.baumGewichten(binaerBaumVar.wurzel);
indem man z.B. zwei Schrägstriche davor setzt, dann entsteht ein ungewichteter sortierter Binärbaum.
In einem neuen Fenster starten: ADT Binärbaum