Wir suchen ein Verfahren, mit welchem ein Text, in welchem praktisch keine Wiederholungen vorkommen, symmetrisch komprimiert abgespeichert werden kann.
- komprimieren = Information wird mit einem bestimmten Algorithmus mit weniger Speicherplatz gespeichert
- symmetrisch = Information kann komprimiert werden und später verlustfrei wieder entkomprimiert (extrahiert) werden
Je nach Codierung kann beim Speichern von Texten viel Speicherplatz notwendig werden.
Gesucht ist eine Codierung von Text, mit welcher Text platzsparend gespeichert werden kann.
Bei einem deutschen Text variiert die Häufigkeit von Buchstaben:
Diese Einsicht führt zur Grundidee der Huffman-Kodierung:
Jedem Zeichen werden nicht immer gleich viele Bit wie z.B. beim UTF-Code zugeordnet, sondern man sucht eine eigene Kodierung, die nur speziell für das Dokument gilt, das man komprimieren möchte. Dabei ist die Codelänge variabel.
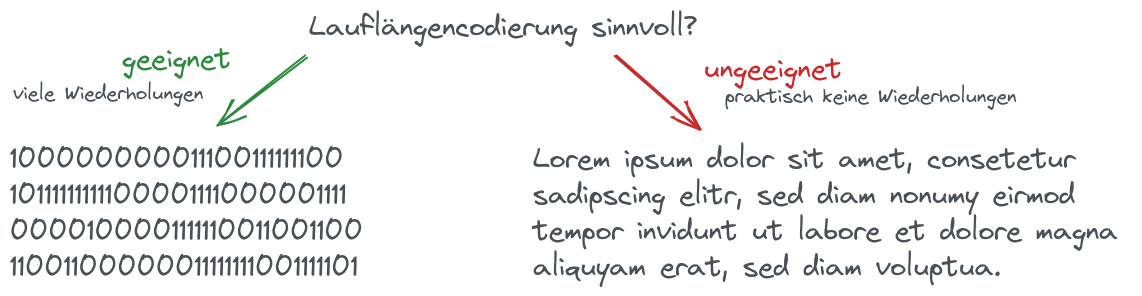
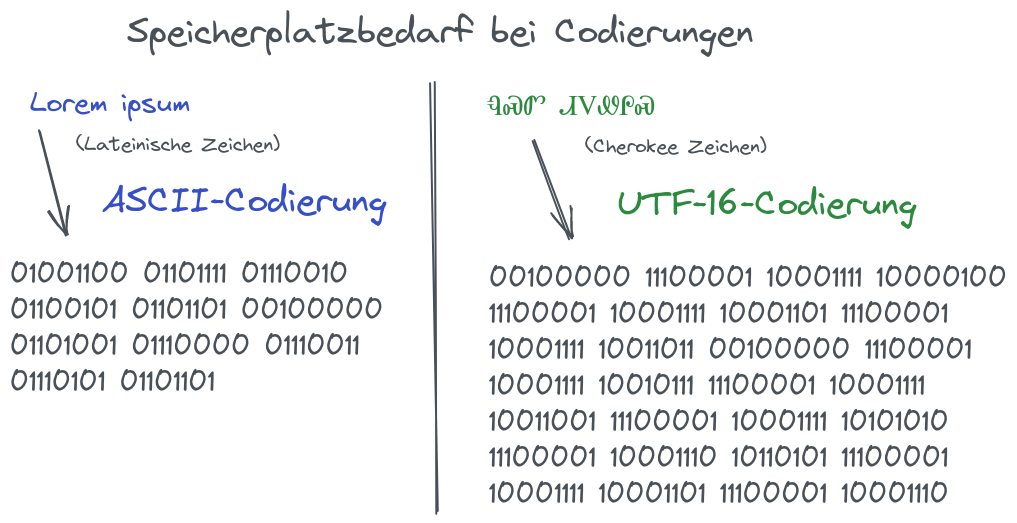
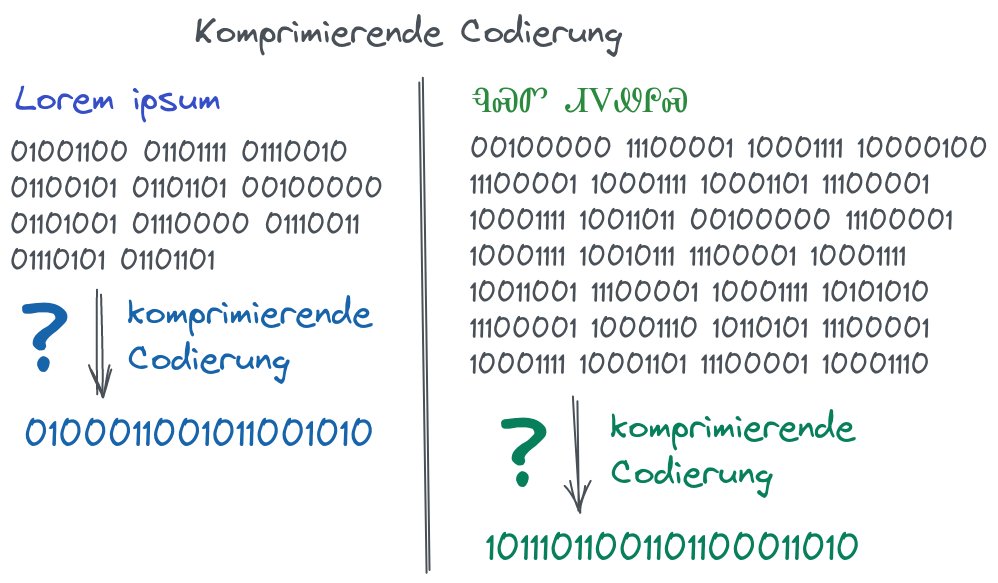
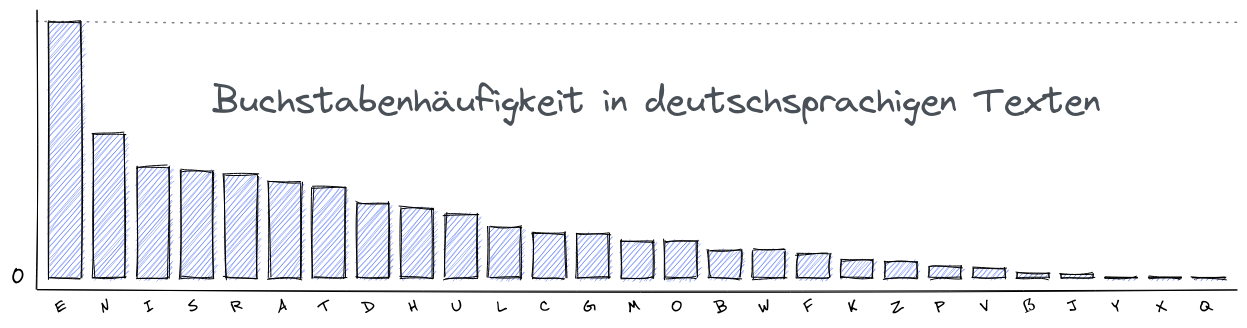
Wie kann ein Text komprimiert werden, so dass der Text wieder eindeutig extrahiert werden kann? Woher soll der Algorithmus wissen, wann ein Zeichen zu Ende ist und das neue Zeichen beginnt. Man könnte die Idee haben ein Trennzeichen einzufügen, das zwei kodierte Bitfolgen voneinander abtrennt. Aber wie soll das Trennzeichen aussehen? Woher weiß der Algorithmus, wann ein Trennzeichen beginnt und eine Zeichen-Bitfolge endet?
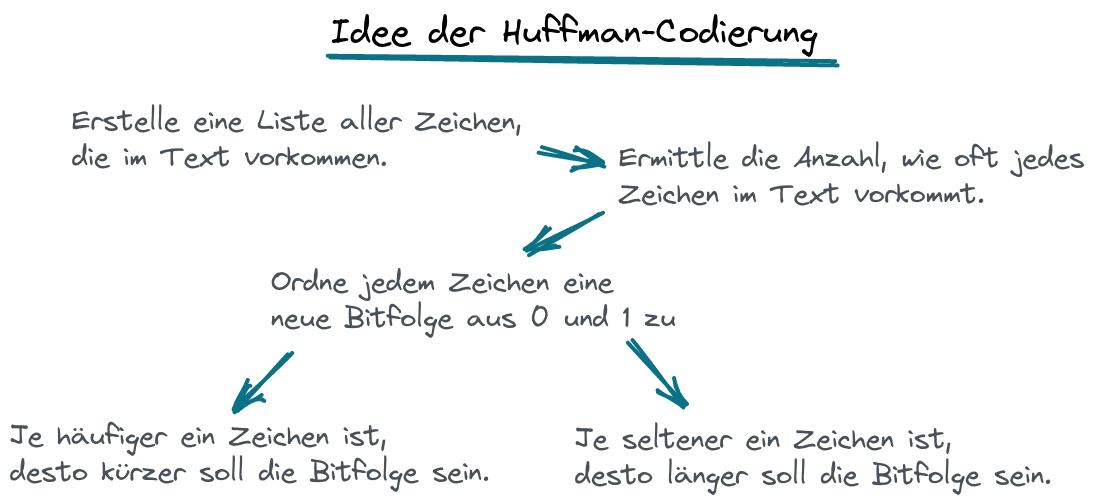
Die Informatiker fanden eine recht einfache Lösung für das Problem: man verwendet kein Trennzeichen, sondern sorgt dafür, dass jedem Zeichen im Text eine Bitfolge zugeordnet wird, die folgenden Regeln genügt:
Jede Bitfolge ist einmalig.
Keine Bitfolge stimmt mit dem Anfang einer anderen Bitfolge überein.
Wenn einer Bitfolge ein Zeichen zugeordnet werden kann, dann beginnt beim nächsten Bit ein neues Zeichen.
Überlegen Sie sich mit Hilfe dieser beiden Regeln eine Kodierung für die Zeichen in "erdbeere", so dass nach einer Kodierung die Extrahierung eindeutig funktionieren kann.
Der typische Ablauf für die Komprimierung eines Textes ist folgender:
Das Auffinden von geeigneten Bitfolgen durch einen Algorithmus ist schwierig. Huffman hatte 1952 einen Algorithmus dafür vorgeschlagen.
Öffnen Sie folgende Internetseite in einem neuen Fenster: Huffman-Kodierung
Geben Sie das Wort "erdbeere" ein, klicken Sie auf "Build tree" und beobachten Sie die Entstehung des binären Baums (eine Struktur, bei der von einem Knoten immer genau zwei weitere Knoten ausgehen). Wenn der Algorithmus hängen bleibt, laden Sie die Seite bitte neu. Wenn der Algorithmus erfolgreich war steht unten die Meldung "Animation Completed".
Überlegen Sie, wie man von diesem binären Baum zu der Code-Zuordnung: "b" = 111; "d" = 110; "r" = 10; "e" = 0, die in der Lösung zur letzten Aufgabe angegeben wurde, kommt.
Nachdem klar ist, wie aus einem Huffman-Baum die Kodierung für einen Text erzeugt wird, fehlt nur noch die Kenntnis darüber, wie der Huffman-Baum erzeugt wird. Das sollen Sie sich mit Hilfe der Animation selbst klar machen.
Öffnen Sie folgende Internetseite in einem neuen Fenster: Huffman-Kodierung
Geben Sie unterschiedliche Worte ein und lassen Sie sich jeweils einen binären Baum erzeugen.
Erstellen Sie in Ihrer Arbeitsgruppe eine Dokumentation in einem Programm Ihrer Wahl zum Thema: Wie wird zu einem gegebenen Text ein Huffman-Baum erzeugt? Legen Sie dazu einen zu komprimierenden Text fest. Der Text sollte mindestens 10 verschiedene Zeichen beinhalten.
Zur Erstellung der Dokumentation können Sie die Pause-Funktion der Animation nutzen und den entstehenden Baum mit Hilfe eines geeigneten Tools in Ihre Dokumentation einfügen. Jeder Schritt sollte zusätzlich zur Bildschirmkopie mit einem kurzen Text erklärt werden.
In einem neuen Tab öffnen: Huffman-Codierung