13.2.2 Endliche Automaten

Ein große Thema in der IT ist heute die Digitalisierung. Viele Abläufe, die früher analog abliefen, sollen in computerbasierte Systeme übertragen werden.

Im Smart-Home werden die Rolläden, die Heizung, der Kühlschrank,... zentral von einer App auf dem Handy überwacht und gesteuert. Die Produktion soll möglichst von autonomen Robotern erledigt werden, autonome Autos sollen durch die Gegend fahren und es wird an autonomen Kampfsystemen gearbeitet, die künftig Soldaten ersetzen sollen.

Wir bekommen die digitale Patientenakte, den digitalen Personalausweis und der Gang zum Amt soll ersetzt werden mit dem Aufrufen der Internetseite des Amts.

Und so weiter...

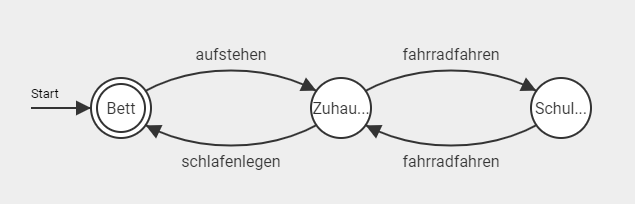
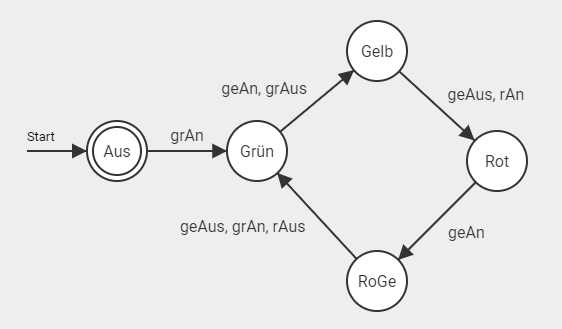
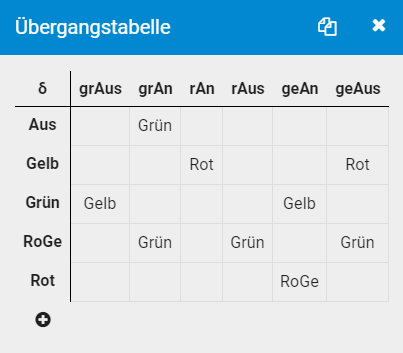
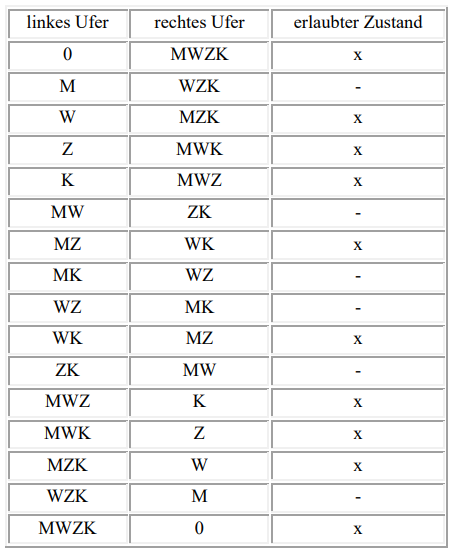
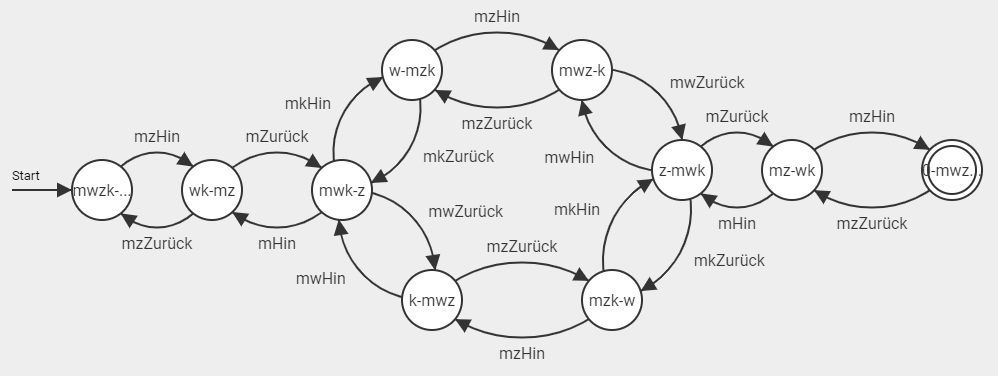
Bevor diese Abläufe digitalisiert werden können, sollte allen Beteiligten klar sein, was überhaupt digitalisiert wird und wie die Abläufe digitalisiert werden sollen. Eine Möglichkeit, diese Abläufe abstrakt zu visualisieren, bevor mit der Digitalisierung begonnen wird, ist es Methoden der Automatentheorie zu verwenden.

In der Automatentheorie beschreiben Zustände das zu modellierende System. Zwischen den Zuständen gibt es Übergänge.

Im ersten Beispiel wird ein extrem vereinfachter Tagesablauf beschrieben. Es gibt 3 Zustände:

• Bett
• Zuhause
• Schule

Die Übergänge zwischen diesen Zuständen sind:

• aufstehen
• schlafenlegen
• fahrradfahren

Mit diesen Zuständen und Übergängen kann der Tagesablauf modelliert werden. Für die Modellierung gibt es zwei Darstellungsmöglichkeiten:

1) Ein Diagramm

2) Eine Tabelle

Spielen können Sie mit diesem Modell unter folgender Adresse: FLACI-Link:

Im zweiten Beispiel wird eine einfache Ampel modelliert. Es gibt fünf Zustände:

• Aus
• Grün leuchtet
• Gelb leuchtet
• Rot leuchtet
• Rot und Gelb leuchtet

Die Übergänge zwischen diesen Zuständen sind:

• grün An
• grün Aus
• gelb An
• gelb Aus
• rot An
• rot Aus

Spielen können Sie mit diesem Modell unter folgender Adresse: FLACI-Link:

Ein Mann steht mit einem Wolf, einer Ziege und einem Kohlkopf am linken Ufer eines Flusses, den er überqueren will. Er hat ein Boot, das groß genug ist, ihn und ein weiteres Objekt zu transportieren, so dass er immer nur einen der drei mit hinübernehmen kann. Falls der Mann allerdings den Wolf und die Ziege unbewacht an einem der Ufer zurücklässt, wird der Wolf sicherlich die Ziege fressen. Genauso wird, wenn die Ziege und der Kohlkopf unbewacht zurückbleiben, die Ziege den Kohlkopf fressen. Ist es möglich, den Fluss zu überqueren, ohne dass die Ziege oder der Kohlkopf gefressen werden?

Die möglichen Zustände bestehen aus der Information, wer mit wem an welchem Ufer steht. Die Übergänge sind die möglichen Fahrten im Boot von einem Ufer zum anderen Ufer. Wenn man alle möglichen Zustände sucht, findet man 16 mögliche Zustände. Davon sind manche erlaubt und andere verboten:

Aus dieser Auswahl überträgt man die erlaubten Zustände und die dazugehörenden Übergänge in ein Diagramm:

FLACI-Link:

Man findet zwei Lösungen, die zur gewünschten Zielsituation führen. Natürlich könnte man auch beliebig oft hin- und herfahren, ohne die Zielsituation zu erreichen, aber diese Lösungen betrachtet man nicht, da sie sinnlos sind.

Das Diagramm kann als Übergangstabelle angegeben werden:

Solche abstrakten Darstellungen von endlich vielen Zuständen und Übergängen zwischen den Zuständen nennt man einen endlichen Automaten.

In diesem Kurs nutzen wir zur Visualisierung und Simulation von endlichen Automaten folgende Software:

FLACI

Den Quellcode für die Automatensimulationssoftware finden Sie auf GitHub: FLACI - Quellcode