13.3.4 Bit-Subtrahierer

Subtrahieren ist Minusrechnen. Sie wissen, dass man jede Subtraktionsaufgabe in eine Additionsaufgabe (Plusrechnen) umwandeln kann, indem man die Gegenzahl addiert.

Beispiel:

\(7 - 3 = 7 + (-3)\)

Die Gegenzahl zu einer gegebenen Zahl findet man, indem man die gegebene Zahl am Zahlenstrahl an der Null spiegelt.

Wenn wir es schaffen, zu einer gegebenen Binärzahl die Gegenzahl (negative Binärzahl) anzugeben, könnten wir aus jeder Subtraktion eine Addition machen. Sobald wir das geschafft haben, könnten wir den Volladierer auch für Subtraktionsaufgaben einsetzen.

Wenn Zahlen im Computer nur mit den beiden Symbolen "1" und "0" angegeben werden, können wir vor eine Zahl nicht einfach ein negatives Vorzeichen setzen, um aus der Zahl eine negative Zahl zu machen, denn wir haben kein drittes Symbol, das wir als negatives Vorzeichen nutzen könnten.

Wir müssen einen Weg finden eine negative Zahl nur mit Hilfe der beiden Symbole "1" und "0" so aufzuschreiben, dass die Addition einer negativen Binärzahl und einer positiven Binärzahlen mit unseren Volladdierern richtige Ergebnisse liefert.

Wir reservieren für eine Binärzahl eine bestimmte Anzahl an Bits, z.B. 4 Bits. Mit 4 Bits können die Zahlen 0; 1; ...; 15 dargestellt werden. Zählen bedeutet, dass man immer die Zahl 1 addiert.

Wenn man mit einer begrenzten Anzahl an verfügbaren Bits zählt, dann entsteht die Frage, was man machen soll, wenn man das Ende der möglichen Zahlen erreicht:

0000; 0001; 0010; ...; 1110; 1111; ?

Da kein weiterer Speicherplatz für die Zahldarstellung verfügbar ist, entsteht durch bei der Addition von \(1111_\rm{2}\) und \(1_\rm{2}\) die 4-Bit-Zahl \(0000_\rm{2}\), da für den Übertrag kein Speicherplatz verfügbar ist.

Für eine endliche Anzahl von Zahlen macht es daher wenig Sinn diese grafisch mit Hilfe einer Zahlengeraden darzustellen, die ja unendlich viel Platz bereithält. Eine sinnvolle mögliche Darstellung der endlichen Anzahl von 4-Bit-Zahlen ist die Darstellung an einem Zahlenkreis:

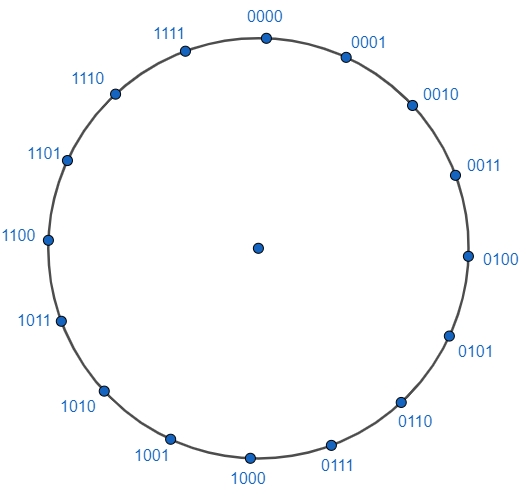
An einer Zahlengeraden trennt die Zahl \(0_\rm{10}\) die positiven Zahlen von den negativen Zahlen. Die negativen Zahlen werden nach links kleiner, die positiven nach rechts größer. Diese Idee kann auf den Zahlenkreis übertragen werden:

Die Zahl \(0000_\rm{2}\) soll die positiven von den negativen Zahlen trennen. Die erste negative Zahl wäre dann die \(1111_\rm{2}\), dann kommt die \(1110_\rm{2}\) und so weiter. Zählen wir weiter in die negative Richtung, also nach links:

Man sieht, dass die Gegenzahlen auf dem Zahlenkreis einander gegenüber stehen.

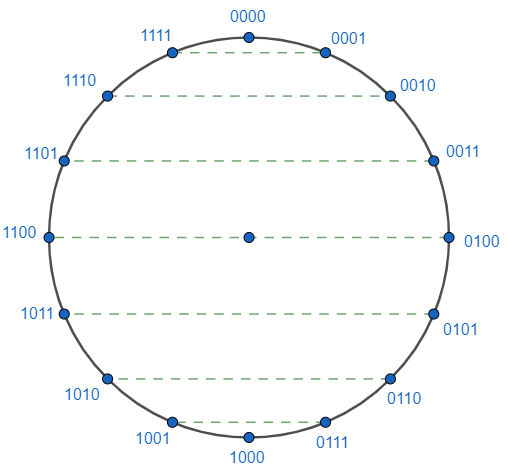
Die Summe einer Zahl und ihrer Gegenzahl muss 0 sein. Man kann leicht nachrechnen, dass das für die gerade gefundenen Binärzahlen und ihre Gegenzahlen zutrifft.

Es ist jetzt aber nicht klar, was man mit der Zahl \(1000_\rm{2}\) machen soll, denn diese kann nach der Bildungsregel im Dezimalsystem die Zahl -8 oder die Zahl 8 sein.

Wenn man den Zahlenkreis ansieht, fällt auf, dass alle negativen Zahlen von -1 bis -7 in der binären Schreibweise eine "1" als linkes Bit haben. Die positiven Zahlen von 1 bis 7 haben ein "0" als linkes Bit.

Wenn man das linke Bit "opfert" und als "Vorzeichen" einführt, kann man die Zahlen von 0 bis 7 und ihre Gegenzahlen mit 4-Bit darstellen. Die Zahl \(1000_\rm{2}\) wäre dann in dezimaler Schreibweise die Zahl -8.

Mit 5 Bit könnte man 1 Bit für das Vorzeichen und 4 Bit für die Zahldarstellung verwenden, so dass man die Zahlen von -16 bis +15 darstellen kann.

Mit 6 Bit kann man die Zahlen von -32 bis +31 darstellen, mit 7 Bit die Zahlen von -64 bis +63 und mit 8 Bit die Zahlen von -128 bis + 127.

Vergleichen wir die positiven Binärzahlen und ihre Gegenzahlen:

Um aus der positiven Binärzahl die Gegenzahl zu machen, kann man wie folgt vorgehen:

• man negiert alle Ziffern der positiven Binärzahl (aus 1 wird 0 und aus 0 wird 1)
• man addiert die Zahl \(1_\rm{2}\) zu der negierten Binärzahl.

Beispiel 1:

• \(0001_\rm{2}\) wird zu \(1110_\rm{2}\)
• \(1110_\rm{2} + 1_\rm{2} = 1111_\rm{2}\) (klappt!)

Beispiel 2:

• \(0110_\rm{2}\) wird zu \(1001_\rm{2}\)
• \(1001_\rm{2} + 1_\rm{2} = 1010_\rm{2}\) (klappt!)

Beispiel 3:

\(01101110_\rm{2} = 110_\rm{10}\)

Die Summe aus einer Zahl und einer Gegenzahl muss 0 sein. Als Gegenzahl zu \(01101110_\rm{2}\) suchen wir den Binärcode, der zu \(0110 1110_\rm{2}\) addiert 0 liefert. Das kann man leicht im Kopf überlegen:

\(01101110_\rm{2} + 10010010_\rm{2} = 0_\rm{2}\)

Also ist die Gegenzahl von \(01101110_\rm{2}\) die Zahl \(10010010_\rm{2}\)

Test, ob das Umwandlungsschema klappt:

• \(01101110_\rm{2}\) wird zu \(10010001_\rm{2}\)
• \(10010001_\rm{2} + 1_\rm{2} = 10010010_\rm{2}\) (klappt!)

Um zwei Binärzahlen voneinander abzuziehen, muss zur zweiten Zahl die Gegenzahl gebildet werden. Die Gegenzahl der zweiten Binärzahl wird dann zur ersten addiert.